Som bekant mår förhållanden bra av ömsesidig kommunikation, där båda sidor lyssnar in och tar lärdom av varandra. Det gäller inte bara mänskliga relationer, utan även vetenskapliga discipliner. Genetik och statistik har under lång tid inspirerat varandra. Utan att göra anspråk på att täcka alla delar av denna interaktion, vill jag med några nedslag i historien och belysa händelser som påverkat ämnenas utveckling, och även peka på några aktuella forskningsområden.
Man kan säga att den moderna genetiken föddes då Georg Mendel på 1860-talet upptäckte att anlag ärvs ned från föräldrar till barn i kvantiteter som i matematisk mening är diskreta. Mendel undersökte olika egenskaper hos ärtväxter. Deras fröer var till exempel antingen släta eller veckade; fröerna uppvisade inte en kontinuerlig skala från att vara släta till att vara veckade. Idag kallar vi de diskreta kvantiteter som ger upphov till sådana egenskaper för gener. Mendels experiment med korsning av ärtväxter ledde bland annat fram till två insikter, den att varje individ bär på en dubbel uppsättning anlag eller genvarianter som erhålls från respektive förälder, och den att endast en av individens två anlag, med samma sannolikhet 0,5, ärvs vidare till nästa generation. Mendel menade att dessa principer borde gälla för alla arter. Eftersom varje gen har ett ändligt antal olika varianter innebar hans teorier att den ärftliga variationen är diskret i matematisk mening.
Två synsätt
Jag ska använda begreppet fenotyp i fortsättningen. Med fenotyp menas en organisms observerbara egenskaper, som till exempel kroppslängd.
Mendels bortglömda teorier återupptäcktes efter sekelskiftet. Snart uppstod en kontrovers mellan de mendelska och biometriska synsätten, eftersom genbegreppet verkade oförenligt med ärftlig variation av kontinuerliga fenotyper, medan blandningshypotesen skulle medföra att ärftlig variation försvann efter några generationer eftersom blandningen då blivit praktiskt taget homogen. Mendel själv och senare Yule hade visserligen föreslagit att kontinuerliga fenotyper kan ses som polygena, dvs att de orsakas av flera gener som ärvs ned oberoende av varandra, var och en med liten effekt.
Det blev dock en ung brittisk forskare vid namn Ronald Fisher som i ett berömt arbete 1918 på ett mer generellt sätt visade hur kontinuerlig anlagsvariation gick att kombinera med det mendelska synsättet. Han delade upp fenotypvariansen i en miljökomponent och ett antal additiva och dominanta genetiska komponenter, och grundlade därmed den kvantitativa genetiken, som fick stor betydelse för bland annat husdjursavel. Lars Rönnegård skrev i Qvintensen nr 1/2013 hur statistiska metoder används idag inom husdjursavel. Men dessa idéer låg även till grund för den variansanalys han senare på 1920-talet utvecklade för försöksplanering inom jordbruket.
Fisher räknas kanske som 1900-talets främste statistiker. Han verkade under en tid när statistikämnet växte fram som en självständig disciplin, både internationellt och i Sverige. Själv var han stora delar av sitt liv professor i genetik, och många av hans statistiska upptäckter, såsom ML-skattningen och det vi numera kallar Fisherinformationen, inspirerades av eller tillämpades på genetiska frågeställningar.
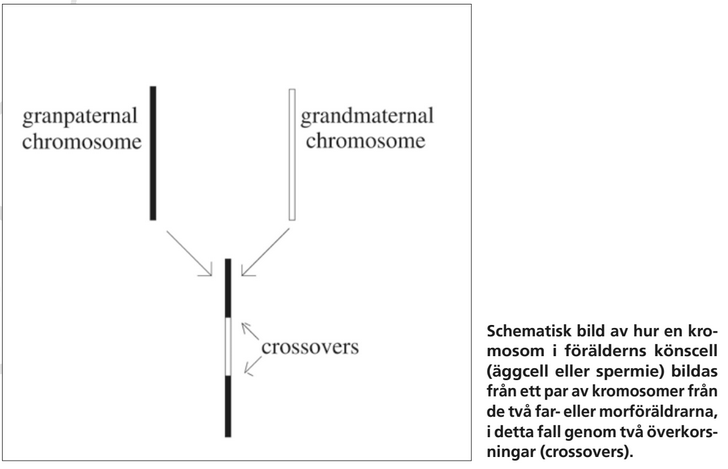
På 1910-talet hade man förstått att gener ligger utplacerade längs kromosomer som för människor utgör 23 par, av vilka ett består av två könskromosomer. Avkomman får ena kromosomen i ett par från sin mamma och den andra kromosomen i paret från pappa. För en icke könskromosom har föräldern i sin tur fått de anlag han eller hon ärver vidare till barnet från sin mamma eller pappa. För gener på olika kromosomer stämmer Mendels hypotes att olika anlag ärvs ned oberoende av varandra. För två gener på samma kromosom är däremot sannolikheten för att barnet får anlag från olika mor- eller farföräldrar (en så kallad rekombination) en funktion av genernas avstånd från varandra. Att barnet inte säkert får alla anlag på en kromosom från mamma från samma morförälder beror på att delar av den kromosom som härrör från morfar kan byta plats med motsvarande del från mormors kromosom när en äggcell bildas. På samma sätt kommer kromosomstycken från farmor och farfar byta plats när en spermiecell bildas hos pappan. Effekten blir att kromosomer i praktiken ärvs ned styckvis från respektive mor- eller farförälder. Om två gener ligger nära varandra är sannolikheten stor att avkomman får båda av dem från samma mor- eller farförälder. Brytpunkterna mellan kromosomstyckena kallas överkorsningar, och J.B.S. Haldane föreslog 1919 att de lämpligen beskrivs av en Poissonprocess.
Haldanes och snarlika modeller för överkorsningar låg till grund för flera av de genletningsmetoder som utvecklades. Gener lokaliserades successivt längs olika arters kromosomer, genom att Fisher och andra utvecklade metoder för att testa om en nyfunnen gen ligger på en viss kromosom, och givet det, bestämma läget för genen genom att ML-skatta sannolikheten att den rekombinerar, dvs har ett udda antal överkorsningar mellan sig och ett kromosomavsnitt som redan positionsbestämts, en så kallad markör. Detta förfarande kallas kopplingsanalys, eftersom markören och genen sägs vara kopplade till varandra om de inte ärvs ned oberoende. För att hitta anlagen för ärftliga mänskliga sjukdomar samlade man in fenotyper och genvarianter för allt större släktträd. Mendels lagar medför att genernas nedärvning i ett släktträd på varje kromosomposition kan beskrivas av en markovsk graf, eftersom vilka gener avkomman får bara beror på de gener som finns i föräldrargenerationen. På 1970-talet utvecklade Robert Elston, Kenneth Lange, Chris Cannings, Elisabeth Thompson och andra sannolikhetsberäkningar på sådana grafer (en föregångare till dagens grafiska modeller och bayesianska nätverk) för att skatta genpositioner.
Med molekylärbiologins landvinningar ökade samtidigt förståelsen för cellens kemiska uppbyggnad. På 1950-talet hade man kommit till insikt om att kromosomerna mellan celldelningar var belägna i cellkärnan, som en dubbelsträngad stege av kvävebaser (DNA-molekylen), där båda strängarna innehåller samma information. I cellerna byggs proteiner upp från beståndsdelar som är aminosyror. Proteiner i kosten spjälkas upp i aminisyror för att senare sättas samman till nya proteiner som behövs i kroppen för en mängd olika uppgifter. Det måste alltså finnas något recept eller instruktion som styr vilka proteiner som kommer till. Några år efter upptäckten av kvävebaserna i DNA hade man förstått att generna utgör kromosomavsnitt som via RNA ger instruktioner för (”kodar för”) cellernas proteinsyntes. Varje instruktion kan beskrivas med trebokstaviga ord som svarar mot olika aminosyror. Dessa insikter möjliggjorde i sin tur en snabb utveckling av gentekniken. Man upptäckte att restriktionsenzymer kan klippa ut DNA-avsnitt, som sedan kunde särskiljas från varandra med elektroforesmetoder. Detta gjorde att data från en snabbt växande karta av genetiska markörer kunde samlas in.
Medan Mendels ärftlighetslagar ger en Markovstruktur över hur gener förs ner genom generationerna, ger Haldanes modell för överkorsningar en annan Markovegenskap för nedärvning, längs kromosomerna. Eftersom de observerade genetiska markörerna ger en bild av denna nedärvning som innehåller stora mått av statistisk osäkerhet, visade bland annat Eric Lander på 1980-talet hur gömda (ej direkt observerbara) Markovkedjor kunde tillämpas för att på ett bättre och mer fullständigt sätt utnyttja informationen från alla markörer. Under 1980-talet och en bit in på 90-talet hittade man de genvarianter som ökar risken för cystisk fibros, Huntingtons sjukdom och ett stort antal andra monogena sjukdomar.
I början av 90-talet sjöd optimismen, snart skulle man finna de genetiska komponenterna hos många betydligt vanligare folksjukdomar, exempelvis åldersdiabetes, Alzheimers sjukdom, multipel skleros, vissa psykiska sjukdomar och olika typer av cancer. För att åstadkomma detta beslutades att hela det mänskliga genomet skulle kartläggas, det så kallade HUGO-projektet. Det tog ett decennium att sekvensera ett prototypgenom med cirka 3 miljarder baspar genom att först sönderdela DNA-strängarna i delvis överlappande små fragment. Med Poissonapproximation uppskattades hur många fragment som krävs för att med stor sannolikhet täcka hela genomet, och sedan användes olika datalogiska metoder för att pussla ihop dem i rätt ordning. Efter HUGO-projektets slutförande i början av 2000-talet har man under mer än ett decennium i de så kallade HapMap och 1000 Genomes-projekten kartlagt de miljontals baspar som är polymorfa, dvs varierar mellan individer och gör oss genetiskt olika som människor.
Med dessa nya data uppstod redan på 1990-talet behov av ny teoriutveckling för genletning, inte minst olika simuleringstekniker som MCMC och vägd simulering, för att hantera stora släktträd, många markörer och ofullständiga data. Trots denna avancerade statistiska teori visade det sig vara mycket svårare att genbestämma folksjukdomarna, eftersom de svarar mot det gamla biometriska synsättet, där ingen enskild gen har en stor effekt. Detsamma gäller många andra komplexa fenotyper, såsom kroppslängd, BMI och olika typer av kognitiv förmåga.
När man genomför många hypotestest i samma studie kommer med stor sannolikhet någon andel av testen visa falska signifikanser. I takt med att markörkartorna för hela genomet blev tätare, började tyvärr alltfler falska positiva fynd med kandidatregioner för sjukdomsgener publiceras. Det blev därför nödvändigt att i kopplingsanalysen korrigera för multipel testning på ett strikt sätt, och eftersom nedärvningen av närliggande markörer är korrelerad, är Bonferronimetoden alldeles för konservativ. Istället använde David Siegmund, Eric Lander och Leonid Kruglyak extremvärdesteori för gaussiska processer för att ange kriterier för när ett kromosomavsnitt kunde rapporteras som ett äkta fynd. Dessa formler för ”familywise error rate” (FWER) är dock approximativa, speciellt när informationen från markörer är ofullständig, och idag används ofta simuleringsmetoder.
I stället för att som i kopplingsanalysen använda data från familjer, kan data bestå av fall och kontroller utan nära släktskap. Man låter markörerna vara kovariater i en logistisk regressionsmodell och testar om de själva (inte deras nedärvning) är associerade med den oberoende variabeln, som anger om individen är sjuk eller ej. Det kallas associationsanalys. Förutom att data för associationsanalysen är lättare att samla in än de data som behövs i kopplingsanalysen, upptäckte Neil Risch och hans medarbetare mot slutet av 90-talet att associationsanalysen ofta har högre styrka än kopplingsanalysen för polygena sjukdomar, där varje riskgen tagen för sig har liten effekt. Detta gäller trots att problemet att välja rätt modell i associationsanalysen är besvärligt, eftersom fler markörer måste undersökas.
Trots associationsstudiernas högre styrka blev det ändå nödvändigt att forskargrupper från många länder bildade konsortier och slog ihop sina dataset, och att markörer som inte var med i en viss studie imputerades från referensgenomen i HapMap eller 1000 Genomes. Detta har många gånger varit framgångsrikt, och man har identifierat tusentals genvarianter som har en statistiskt signifikant (men oftast marginell) association med totalt flera hundra komplexa sjukdomar eller andra fenotyper. Statistisk association är dock inte samma sak som kausalitet, och för de flesta av dessa genvarianter återstår att förklara varför de höjer risken för sjukdomen. Dessutom försvåras sådana internationella metastudier av att gener kan i olika grad vara associerade med sjukdomen i olika populationer (heterogenitet), och att associationsanalysen har svårigheter att upptäcka ovanliga genvarianter. För att även utnyttja de insamlade familjedata som faktiskt finns, används därför kopplingsanalysen ibland som ett komplement till eller tillsammans med associationsanalysen.
Men data från HUGO-projektet användes också tillsammans med dess efterföljare för andra arter för att gruppera DNA-sekvenser (eller aminosyresekvenser) med liknande utseende hos olika arter, för att bland annat förstå funktionen hos de proteiner de kodar för. Detta kan åstadkommas med gömda Markovmodeller, medan programpaketet BLAST använder andra stokastiska metoder (utvecklade av bland annat Samuel Karlin och Stephen Altschul) för att avgöra om likhet mellan olika sekvenser är signifikant. Detta innefattar extremvärdesteori för exkursioner av slumpvandringar med negativ drift, förnyelseteori och sekventiella tester. Jag skrev om detta i Qvartilen år 2004.
En annan viktig utveckling var när man mot slutet av 1990-talet hittade storskaliga metoder för så kallad mikroarrayanalys, med syftet att bestämma vilka gener som är aktiva i olika celler med att uttrycka sin proteinkod. För att hitta riskgener för sjukdomar är det framför allt skillnaden i genaktivitet mellan sjuka och friska individer i den för sjukdomen aktuella cellvävnaden som är intressant. Dessa nya data ledde till vidareutveckling av Robert Tibshiranis lasso och andra metoder för att skatta effekter i regressionsmodeller där antal prediktorer (t ex antalet undersökta gener) är större än antal observationer (exempelvis antal individer). Även teorin för multipla tester fördes framåt. Eftersom FWER är ett alldeles för konservativt kriterium för mikroarrayanalys, används istället ofta bayesianska metoder eller False Disovery Rates, och genom arbeten av bland annat Sandrine Dudoit, Terry Speed och John Storey har förståelsen multipel testning i allmänhet och FDR i synnerhet ökat. En modern efterföljare till mikroarrayanalys, så kallad RNA-sekvensering, har ibland visat sig vara ett mer flexibelt sätt att upptäcka fler typer av genaktivitet, och även deras dynamik. För denna typ av data består genuttrycken av en multivariat tidsserie, och att analysera dem innebär nya statistiska utmaningar.
Bara de senaste 15 åren har den moderna biologin utvecklats mycket snabbt. ENCODE-projektet i början på 2000-talet visade att icke-kodande DNA, som finns mellan generna och som upptar drygt 98 % av genomet, verkar ha en mängd viktiga funktioner, bland annat för genreglering med hjälp av så kallade transkriptionsfaktorer eller mikro-RNA. Det är möjligt att flera av de genvarianter som hittats med associationsstudier snarare ligger nära men utanför en gen eller i en icke-kodande del av genen. I båda fallen är det genens grad av aktivitet som påverkas, snarare än vilket protein den kodar för. Här kan även stokastisk automatteori och andra matematiska verktyg få betydelse för att i mer detalj beskriva informationen hos den icke-kodande DNA-strängen. Den transkription av DNA-strängar som ligger till grund för proteinsyntesen är mycket mer raffinerad och komplicerad än man tidigare trott, eftersom en gen kan koda för flera proteiner, beroende på varifrån och i vilken riktning avläsningen sker. Dessutom har epigenetiken visat att förmågor som förvärvats under livet i vissa fall kan ärvas vidare till nästa generation, bland annat genom förändringar i de proteinkomplex (histoner) som DNA-molekylerna är virade kring.
Den nya kunskapen om DNA-strängar integreras alltmer med ökad förståelse av hur en cell fungerar. Det eller de proteiner en gen kodar för ingår i ett antal kemiska reaktioner. Varje cell kan liknas vid en hel stad av aktivitet, där systembiologin ger utmärkta verktyg för att beskriva de processer för ämnesomsättning, kraftproduktion, lagring av restprodukter och transport som pågår. Även här har statistiken en viktig roll att spela, t ex associationsstudier mellan genetiska markörer och olika multivariata fenotyper på cellnivå, såsom genuttryck, proteinsekvenser och metabolism. När sådana ”big data” analyseras får man ännu större problem med multipla tester, inte minst när olika typer av data kombineras. Men även stokastisk reglerteori, dynamiska bayesianska nätverk och olika hierarkiska modeller är väl lämpade för att beskriva sådana komplexa system. För vissa bayesianska modeller är likelihoodfunktionen så svår att beräkna att den måste approximeras med simuleringar (så kallade ABC-metoder). Men ibland är approximativa och enklare modeller mer praktiskt användbara, dels för att de är mindre beräkningsintensiva, dels för att de är robustare mot felaktiga modellantaganden.
Det jag hittills beskrivit är hur den genetiska kunskapen ökat under 150 år, både vad gäller kartläggning av gener, vilka varianter som finns av dem och vilken funktion de har. Den kanske viktigaste användningen av denna kunskap är att skräddarsy medicin, genterapi och andra behandlingsmetoder för olika människor. Vi är fortfarande bara i början på denna utveckling, där man snabbt kommer in på etiska frågeställningar när den personliga integriteten ska avvägas mot användande av mer eller mindre kodad genetisk information. Rent statistiskt kan DNA, genaktivitet, metabolism och andra biomarkörer i olika celler ses som kovariater eller prediktorer i en regressionsmodell, där effekten av en viss medicin blir responsvariabel. För att öka förståelsen av sambandet mellan riskfaktorerna kan kausal inferens vara användbart, ett område där bland annat Donald Rubin gjort viktiga bidrag.
För modeller med mutationer blir tillståndsrummet mer komplicerat, eftersom nya genvarianter tillkommer. Men delar in de N individerna i ekvivalensklasser beroende på deras genvariant, och låter Xt beskriva tidsdynamiken hos klasstorlekarnas fördelning. Warren Ewens angav i början av 1970-talet en samplingformel, som under vissa antaganden ger jämviktsfördelningen hos selektivt neutrala genvarianter i närvaro av mutationer. Den uppstår som en balans mellan de två mekanismer som strävar efter att minska (genetisk drift) respektive öka (mutationer) den genetiska variationen. Rekombinationer, slutligen, införs när den genetiska variationens tidsutveckling studeras för flera markörer samtidigt, så att Xt blir en vektor där varje element svarar mot en markör.
Hittills har ”tiden” t bara varit en räknare för generation. För stora populationer är det ofta en fördel att införa kontinuerlig tid och approximera Markovkedjan med en stokastisk differentialekvation. Om vi undersöker flera genpositioner samtidigt blir denna SDE vektorvärd, där A) den genetiska driften och rekombinationerna ger elementen i diffusionstermens kovariansmatris, och B) det naturliga urvalet och migrationen orsakar den systematiska driften. Om vi dessutom utökar modellen till att innehålla mutationer blir tillståndsrummet mer komplicerat, som i det tidsdiskreta fallet. Medan Fisher lade grunden för SDE-approximationerna, utvecklade Wright denna teknik vidare, och sedan tog Kimura vid och löste på 1950-talet Kolmogorovs framåt- och bakåtekvationer explicit i flera viktiga fall.
I slutet av 1970-talet skrev Ewens en bok som sammanfattade mycket av den dittills utvecklade matematiska teorin för populationsgenetik. Kort därefter introducerade John Kingman i början av 1980-talet en idé som visade sig vara mycket fruktbar för populationsgenetiken. Hans koalescensteori kan sägas vara en vidareutveckling av att vända på tiden för en Markovkedja. Vi får då en ny Markovkedja. Visserligen hade Charles Cotterman och Gustave Malécot mer än 30 år tidigare infört begreppet identisk härkomst för gener, men Kingman visade hur ett helt genetiskt släktträd är fördelat bakåt i tiden. Detta släktträd är inte en vanlig individbaserad stamtavla, utan ett Markovträd som visar hur olika individers kopior av en gen har ärvts ned längs olika släktlinjer som så småningom sammanstrålar hos en gemensam anfader. Dess utseende beror inte bara på den kromosom vid vilken genen är belägen, utan även (på grund av överkorsningar) på positionen längs denna kromosom. En av de största fördelarna med koalescensteorin är att selektivt neutrala modeller blir mycket enklare att analysera, eftersom endast de mutationer som överlevt till dagens generation tas med, och de kan slumpas ut som en Poissonprocess på släktträdet.
Koalescensteorin har idag utvecklats till en egen disciplin inom sannolikhetsteorin, där Jean Bertoin, Peter Donnelly, Richard Durrett, Simon Tavaré och andra gjort viktiga bidrag, men även flera svenskar, såsom Magnus Nordborg, Peter Jagers, Ingemar Kaj och Serik Sagitov. Den har många tillämpningsområden, och inom populationsgenetiken är den ett fruktbart verktyg för att studera mänsklighetens historia och andra processer bakåt i tiden, där moderna dataset med hundratusentals markörer per individ ger nya möjligheter att jämföra olika modeller. Något mer överraskande är koalescensteorin även mycket användbar för att studera förändringar framåt i tiden, Den kan exempelvis ge framåtrekursioner för den predikterade inavelskoefficienten
ft=P(samma genvariant för två slumpmässigt valda individer, tid t)
och andra av Wright införda storheter. Liksom i filmen Tillbaka till framtiden kan vi med tidsmaskinens hjälp bygga upp (sannolikhetsfördelningen för) ett släktträd bakåt, med start i framtiden.
Inom bevarandebiologin studerar man hur den biologiska mångfalden i olika ekosystem kan bevaras. Bara de senaste decennierna har många djurarter antingen dött ut eller blivit starkt hotade, bland annat på grund av ökad inavel som ökar förekomsten av recessiva sjukdomar. För att förhindra detta vill man kunna förutsäga risken för att olika anlagsvarianter går förlorade och hur olika strategier påverkar inavelsförändringen (som djurreservat, fiske, fiskodling, anläggning av dammar, avskjutning av älgar, migration av vargar från Finland och Ryssland). Under det korta tidsperspektiv det här är fråga om är det framför allt genetisk drift, migration och rekombinationer som påverkar. Dessutom verkar de kontinuerliga SDE-approximationerna ofta över för lång tid för att vara användbara. Eftersom risken för ökad inavel är större för små populationer än för stora, används den effektiva populationsstorleken Ne som ett mått på inversen av den takt med vilken inaveln ökar. En vanlig tumregel är Ne≥50 för kortsiktigt bevarande av en population 5-10 generationer framåt i tiden.
Man kan ange Ne på flera olika sätt. En metod är att utgå från hur snabbt sannolikheten ft ökar mot 1. Alternativt kvantifierar man hur snabbt genetisk drift sker. För en genetisk markör med två varianter, blir Ne då inversen av en normaliserad varians
σ2=Var(Xt+1Xt(N-Xt)|Xt)=1Ne,
som kan liknas vid volatiliteten för de processer som studeras i finansiell matematik. En tredje metod utgår från största egenvärdet mindre än 1 hos övergångsmatrisen för Markovkedjan Xt. Det anger hur snabbt ett absorberande tillstånd nås: I ett absorberande tillstånd stannar Markovkedjan där den är och därmed har anlag förlorats. Ett fjärde sätt är att med hjälp av koalescensteorin ange hur snabbt grenarna i trädet går ihop bakåt i tiden. Det visar sig att alla dessa definitioner av Ne överensstämmer med den verkliga populationsstorleken N för WF-modellen. Men oftast är Ne betydligt mindre, speciellt om reproduktiviteten mellan föräldrar varierar mer än vad (1) anger.
Under de senaste åren har jag i min forskning arbetat med att få fram en enhetlig matematisk teori för populationer som av någon orsak är strukturerade. Såväl Markovkedjan Xt som den deterministiska inavelsprocessen ft blir då vektorvärda, och definitionerna av effektiv storlek ger olika värden på Ne. Till exempel visar det sig att alla komponenter hos ft-processen går mot 1 med samma hastighet, och den ges av största egenvärdet hos den matris som ligger till grund för tidsrekursionen från ft till ft+1. Men för kortare tidsperspektiv är det mer intressant att ange hela tidsprofilen för inavelsökningen, och då tar man med matrisens hela spektrum av egenvärden. En del av detta, och annat, beskrivs i den avhandling som Fredrik Olsson försvarade i maj 2015, ett arbete som utförts i samarbete med två populationsgenetiker från Stockholms universitet, Linda Laikre och Nils Ryman.
Ola Hössjer
Stockholms universitet
Skriv ut......
Fisher räknas kanske som 1900-talets främste statistiker. Han verkade under en tid när statistikämnet växte fram som en självständig disciplin, både internationellt och i Sverige. Själv var han stora delar av sitt liv professor i genetik, och många av hans statistiska upptäckter, såsom ML-skattningen och det vi numera kallar Fisherinformationen, inspirerades av eller tillämpades på genetiska frågeställningar.
Överkorsningar
På 1910-talet hade man förstått att gener ligger utplacerade längs kromosomer som för människor utgör 23 par, av vilka ett består av två könskromosomer. Avkomman får ena kromosomen i ett par från sin mamma och den andra kromosomen i paret från pappa. För en icke könskromosom har föräldern i sin tur fått de anlag han eller hon ärver vidare till barnet från sin mamma eller pappa. För gener på olika kromosomer stämmer Mendels hypotes att olika anlag ärvs ned oberoende av varandra. För två gener på samma kromosom är däremot sannolikheten för att barnet får anlag från olika mor- eller farföräldrar (en så kallad rekombination) en funktion av genernas avstånd från varandra. Att barnet inte säkert får alla anlag på en kromosom från mamma från samma morförälder beror på att delar av den kromosom som härrör från morfar kan byta plats med motsvarande del från mormors kromosom när en äggcell bildas. På samma sätt kommer kromosomstycken från farmor och farfar byta plats när en spermiecell bildas hos pappan. Effekten blir att kromosomer i praktiken ärvs ned styckvis från respektive mor- eller farförälder. Om två gener ligger nära varandra är sannolikheten stor att avkomman får båda av dem från samma mor- eller farförälder. Brytpunkterna mellan kromosomstyckena kallas överkorsningar, och J.B.S. Haldane föreslog 1919 att de lämpligen beskrivs av en Poissonprocess.
Haldanes och snarlika modeller för överkorsningar låg till grund för flera av de genletningsmetoder som utvecklades. Gener lokaliserades successivt längs olika arters kromosomer, genom att Fisher och andra utvecklade metoder för att testa om en nyfunnen gen ligger på en viss kromosom, och givet det, bestämma läget för genen genom att ML-skatta sannolikheten att den rekombinerar, dvs har ett udda antal överkorsningar mellan sig och ett kromosomavsnitt som redan positionsbestämts, en så kallad markör. Detta förfarande kallas kopplingsanalys, eftersom markören och genen sägs vara kopplade till varandra om de inte ärvs ned oberoende. För att hitta anlagen för ärftliga mänskliga sjukdomar samlade man in fenotyper och genvarianter för allt större släktträd. Mendels lagar medför att genernas nedärvning i ett släktträd på varje kromosomposition kan beskrivas av en markovsk graf, eftersom vilka gener avkomman får bara beror på de gener som finns i föräldrargenerationen. På 1970-talet utvecklade Robert Elston, Kenneth Lange, Chris Cannings, Elisabeth Thompson och andra sannolikhetsberäkningar på sådana grafer (en föregångare till dagens grafiska modeller och bayesianska nätverk) för att skatta genpositioner.
Upptäckten av DNA-molekylen
Med molekylärbiologins landvinningar ökade samtidigt förståelsen för cellens kemiska uppbyggnad. På 1950-talet hade man kommit till insikt om att kromosomerna mellan celldelningar var belägna i cellkärnan, som en dubbelsträngad stege av kvävebaser (DNA-molekylen), där båda strängarna innehåller samma information. I cellerna byggs proteiner upp från beståndsdelar som är aminosyror. Proteiner i kosten spjälkas upp i aminisyror för att senare sättas samman till nya proteiner som behövs i kroppen för en mängd olika uppgifter. Det måste alltså finnas något recept eller instruktion som styr vilka proteiner som kommer till. Några år efter upptäckten av kvävebaserna i DNA hade man förstått att generna utgör kromosomavsnitt som via RNA ger instruktioner för (”kodar för”) cellernas proteinsyntes. Varje instruktion kan beskrivas med trebokstaviga ord som svarar mot olika aminosyror. Dessa insikter möjliggjorde i sin tur en snabb utveckling av gentekniken. Man upptäckte att restriktionsenzymer kan klippa ut DNA-avsnitt, som sedan kunde särskiljas från varandra med elektroforesmetoder. Detta gjorde att data från en snabbt växande karta av genetiska markörer kunde samlas in.
2 gånger Markov
Medan Mendels ärftlighetslagar ger en Markovstruktur över hur gener förs ner genom generationerna, ger Haldanes modell för överkorsningar en annan Markovegenskap för nedärvning, längs kromosomerna. Eftersom de observerade genetiska markörerna ger en bild av denna nedärvning som innehåller stora mått av statistisk osäkerhet, visade bland annat Eric Lander på 1980-talet hur gömda (ej direkt observerbara) Markovkedjor kunde tillämpas för att på ett bättre och mer fullständigt sätt utnyttja informationen från alla markörer. Under 1980-talet och en bit in på 90-talet hittade man de genvarianter som ökar risken för cystisk fibros, Huntingtons sjukdom och ett stort antal andra monogena sjukdomar.
I början av 90-talet sjöd optimismen, snart skulle man finna de genetiska komponenterna hos många betydligt vanligare folksjukdomar, exempelvis åldersdiabetes, Alzheimers sjukdom, multipel skleros, vissa psykiska sjukdomar och olika typer av cancer. För att åstadkomma detta beslutades att hela det mänskliga genomet skulle kartläggas, det så kallade HUGO-projektet. Det tog ett decennium att sekvensera ett prototypgenom med cirka 3 miljarder baspar genom att först sönderdela DNA-strängarna i delvis överlappande små fragment. Med Poissonapproximation uppskattades hur många fragment som krävs för att med stor sannolikhet täcka hela genomet, och sedan användes olika datalogiska metoder för att pussla ihop dem i rätt ordning. Efter HUGO-projektets slutförande i början av 2000-talet har man under mer än ett decennium i de så kallade HapMap och 1000 Genomes-projekten kartlagt de miljontals baspar som är polymorfa, dvs varierar mellan individer och gör oss genetiskt olika som människor.
Enorma mängder av data medför nya problem
Med dessa nya data uppstod redan på 1990-talet behov av ny teoriutveckling för genletning, inte minst olika simuleringstekniker som MCMC och vägd simulering, för att hantera stora släktträd, många markörer och ofullständiga data. Trots denna avancerade statistiska teori visade det sig vara mycket svårare att genbestämma folksjukdomarna, eftersom de svarar mot det gamla biometriska synsättet, där ingen enskild gen har en stor effekt. Detsamma gäller många andra komplexa fenotyper, såsom kroppslängd, BMI och olika typer av kognitiv förmåga.
När man genomför många hypotestest i samma studie kommer med stor sannolikhet någon andel av testen visa falska signifikanser. I takt med att markörkartorna för hela genomet blev tätare, började tyvärr alltfler falska positiva fynd med kandidatregioner för sjukdomsgener publiceras. Det blev därför nödvändigt att i kopplingsanalysen korrigera för multipel testning på ett strikt sätt, och eftersom nedärvningen av närliggande markörer är korrelerad, är Bonferronimetoden alldeles för konservativ. Istället använde David Siegmund, Eric Lander och Leonid Kruglyak extremvärdesteori för gaussiska processer för att ange kriterier för när ett kromosomavsnitt kunde rapporteras som ett äkta fynd. Dessa formler för ”familywise error rate” (FWER) är dock approximativa, speciellt när informationen från markörer är ofullständig, och idag används ofta simuleringsmetoder.
Analys i annan ledd
I stället för att som i kopplingsanalysen använda data från familjer, kan data bestå av fall och kontroller utan nära släktskap. Man låter markörerna vara kovariater i en logistisk regressionsmodell och testar om de själva (inte deras nedärvning) är associerade med den oberoende variabeln, som anger om individen är sjuk eller ej. Det kallas associationsanalys. Förutom att data för associationsanalysen är lättare att samla in än de data som behövs i kopplingsanalysen, upptäckte Neil Risch och hans medarbetare mot slutet av 90-talet att associationsanalysen ofta har högre styrka än kopplingsanalysen för polygena sjukdomar, där varje riskgen tagen för sig har liten effekt. Detta gäller trots att problemet att välja rätt modell i associationsanalysen är besvärligt, eftersom fler markörer måste undersökas.
Trots associationsstudiernas högre styrka blev det ändå nödvändigt att forskargrupper från många länder bildade konsortier och slog ihop sina dataset, och att markörer som inte var med i en viss studie imputerades från referensgenomen i HapMap eller 1000 Genomes. Detta har många gånger varit framgångsrikt, och man har identifierat tusentals genvarianter som har en statistiskt signifikant (men oftast marginell) association med totalt flera hundra komplexa sjukdomar eller andra fenotyper. Statistisk association är dock inte samma sak som kausalitet, och för de flesta av dessa genvarianter återstår att förklara varför de höjer risken för sjukdomen. Dessutom försvåras sådana internationella metastudier av att gener kan i olika grad vara associerade med sjukdomen i olika populationer (heterogenitet), och att associationsanalysen har svårigheter att upptäcka ovanliga genvarianter. För att även utnyttja de insamlade familjedata som faktiskt finns, används därför kopplingsanalysen ibland som ett komplement till eller tillsammans med associationsanalysen.
Men data från HUGO-projektet användes också tillsammans med dess efterföljare för andra arter för att gruppera DNA-sekvenser (eller aminosyresekvenser) med liknande utseende hos olika arter, för att bland annat förstå funktionen hos de proteiner de kodar för. Detta kan åstadkommas med gömda Markovmodeller, medan programpaketet BLAST använder andra stokastiska metoder (utvecklade av bland annat Samuel Karlin och Stephen Altschul) för att avgöra om likhet mellan olika sekvenser är signifikant. Detta innefattar extremvärdesteori för exkursioner av slumpvandringar med negativ drift, förnyelseteori och sekventiella tester. Jag skrev om detta i Qvartilen år 2004.
Det hänger inte bara på vad genen gör utan även på hur aktivt den jobbar
En annan viktig utveckling var när man mot slutet av 1990-talet hittade storskaliga metoder för så kallad mikroarrayanalys, med syftet att bestämma vilka gener som är aktiva i olika celler med att uttrycka sin proteinkod. För att hitta riskgener för sjukdomar är det framför allt skillnaden i genaktivitet mellan sjuka och friska individer i den för sjukdomen aktuella cellvävnaden som är intressant. Dessa nya data ledde till vidareutveckling av Robert Tibshiranis lasso och andra metoder för att skatta effekter i regressionsmodeller där antal prediktorer (t ex antalet undersökta gener) är större än antal observationer (exempelvis antal individer). Även teorin för multipla tester fördes framåt. Eftersom FWER är ett alldeles för konservativt kriterium för mikroarrayanalys, används istället ofta bayesianska metoder eller False Disovery Rates, och genom arbeten av bland annat Sandrine Dudoit, Terry Speed och John Storey har förståelsen multipel testning i allmänhet och FDR i synnerhet ökat. En modern efterföljare till mikroarrayanalys, så kallad RNA-sekvensering, har ibland visat sig vara ett mer flexibelt sätt att upptäcka fler typer av genaktivitet, och även deras dynamik. För denna typ av data består genuttrycken av en multivariat tidsserie, och att analysera dem innebär nya statistiska utmaningar.
Skräpgenerna har visat sig vara viktiga
Bara de senaste 15 åren har den moderna biologin utvecklats mycket snabbt. ENCODE-projektet i början på 2000-talet visade att icke-kodande DNA, som finns mellan generna och som upptar drygt 98 % av genomet, verkar ha en mängd viktiga funktioner, bland annat för genreglering med hjälp av så kallade transkriptionsfaktorer eller mikro-RNA. Det är möjligt att flera av de genvarianter som hittats med associationsstudier snarare ligger nära men utanför en gen eller i en icke-kodande del av genen. I båda fallen är det genens grad av aktivitet som påverkas, snarare än vilket protein den kodar för. Här kan även stokastisk automatteori och andra matematiska verktyg få betydelse för att i mer detalj beskriva informationen hos den icke-kodande DNA-strängen. Den transkription av DNA-strängar som ligger till grund för proteinsyntesen är mycket mer raffinerad och komplicerad än man tidigare trott, eftersom en gen kan koda för flera proteiner, beroende på varifrån och i vilken riktning avläsningen sker. Dessutom har epigenetiken visat att förmågor som förvärvats under livet i vissa fall kan ärvas vidare till nästa generation, bland annat genom förändringar i de proteinkomplex (histoner) som DNA-molekylerna är virade kring.
Den nya kunskapen om DNA-strängar integreras alltmer med ökad förståelse av hur en cell fungerar. Det eller de proteiner en gen kodar för ingår i ett antal kemiska reaktioner. Varje cell kan liknas vid en hel stad av aktivitet, där systembiologin ger utmärkta verktyg för att beskriva de processer för ämnesomsättning, kraftproduktion, lagring av restprodukter och transport som pågår. Även här har statistiken en viktig roll att spela, t ex associationsstudier mellan genetiska markörer och olika multivariata fenotyper på cellnivå, såsom genuttryck, proteinsekvenser och metabolism. När sådana ”big data” analyseras får man ännu större problem med multipla tester, inte minst när olika typer av data kombineras. Men även stokastisk reglerteori, dynamiska bayesianska nätverk och olika hierarkiska modeller är väl lämpade för att beskriva sådana komplexa system. För vissa bayesianska modeller är likelihoodfunktionen så svår att beräkna att den måste approximeras med simuleringar (så kallade ABC-metoder). Men ibland är approximativa och enklare modeller mer praktiskt användbara, dels för att de är mindre beräkningsintensiva, dels för att de är robustare mot felaktiga modellantaganden.
Det jag hittills beskrivit är hur den genetiska kunskapen ökat under 150 år, både vad gäller kartläggning av gener, vilka varianter som finns av dem och vilken funktion de har. Den kanske viktigaste användningen av denna kunskap är att skräddarsy medicin, genterapi och andra behandlingsmetoder för olika människor. Vi är fortfarande bara i början på denna utveckling, där man snabbt kommer in på etiska frågeställningar när den personliga integriteten ska avvägas mot användande av mer eller mindre kodad genetisk information. Rent statistiskt kan DNA, genaktivitet, metabolism och andra biomarkörer i olika celler ses som kovariater eller prediktorer i en regressionsmodell, där effekten av en viss medicin blir responsvariabel. För att öka förståelsen av sambandet mellan riskfaktorerna kan kausal inferens vara användbart, ett område där bland annat Donald Rubin gjort viktiga bidrag.
Förändringar av den genetiska variationen i en hel population
En annan viktig frågeställning är hur den genetiska variationen i en hel population eller art förändras över tid. Populationsgenetiken började utvecklades redan på 1920- och 1930-talen för att besvara just denna fråga. Avgörande insatser gjordes av Fisher, Haldane och Sewall Wright för att kartlägga de byggstenar som driver fram förändringar i form av 1) genetisk drift, dvs slumpvariation med avseende på vilken av de två mor- eller farföräldrarna som ärver ned ett anlag till ett barnbarn, 2) mutationer, dvs förändringar i DNA då könsceller bildas, 3) naturligt urval, dvs en selektiv reproduktiv fördel för individer med vissa genvarianter, 4) rekombination av DNA genom överkorsningar, och 5) migration, dvs genutbyte mellan individer från olika delpopulationer. Av dessa mekanismer är det bara mutationerna, och i viss mån rekombinationerna, som kan medföra att nya genvarianter bildas. Eftersom de allra flesta mutationerna dessutom är neutrala eller skadliga, föreslog Motoo Kimura på 1970-talet att genetisk drift är en viktigare mekanism för att förklara genetiska förändringar än naturligt urval. Observera att genetiker och sannolikhetsteoretiker lägger in helt olika betydelser i ordet drift, något som till en början är förvillande för den som är driftig nog att läsa arbeten från båda disciplinerna.
Populationsgenetiken använder flitigt redskap från sannolikhetsteori och stokastiska processer. Jag nämnde ovan att nedärvning i ett släktträd kan beskrivas av en markovsk graf över generationer. Men då släktförhållandena sällan är kända i en hel population, brukar man istället använda förenklade Markovkedjor för att beskriva hur den genetiska sammansättningen ändras framåt i tiden t. I den enklaste enkönade Wright-Fisher modellen (WF) är genetisk drift den enda förändringsmekanismen. Den utgår från en selektivt neutral gen eller genetisk markör med två varianter (I och II), utan nya mutationer. Populationsstorleken N antas vara konstant och tiden räknas i generationer, där antalet kopior
Xt+1~Bin(N,XtN) (1)
av I ändras från en generation till nästa genom att barnen slumpmässigt med återläggning drar sina föräldrar, så att Xt bildar en Markovkedja. Samuel Karlin och Chris Cannings utvecklade sedan mer allmänna modeller, där antalet ”barn” till föräldrarna i generation t också är utbytbara stokastiska variabler, men med större variation än den som följer av (1). Man kan generalisera modellen och låta populationsstorleken variera över tid. Selektion införs i WF-modellen genom att låta genvariant I ha en reproduktiv fördel s > 0 och låta sannolikheten i (1) bli proportionell mot (1+s)XtN+(1-XtN). För att bygga in migration måste man införa geografisk struktur, exempelvis i form av delvis isolerade öar med ett visst genutbyte emellan. Men man kan även införa andra typer av struktur, såsom ålder (genom att definiera livslängdstabeller, på liknande sätt som i livförsäkring), eller kön (genom de mendelska nedärvningslagarna och olika parningsmönster).
Populationsgenetiken använder flitigt redskap från sannolikhetsteori och stokastiska processer. Jag nämnde ovan att nedärvning i ett släktträd kan beskrivas av en markovsk graf över generationer. Men då släktförhållandena sällan är kända i en hel population, brukar man istället använda förenklade Markovkedjor för att beskriva hur den genetiska sammansättningen ändras framåt i tiden t. I den enklaste enkönade Wright-Fisher modellen (WF) är genetisk drift den enda förändringsmekanismen. Den utgår från en selektivt neutral gen eller genetisk markör med två varianter (I och II), utan nya mutationer. Populationsstorleken N antas vara konstant och tiden räknas i generationer, där antalet kopior
Xt+1~Bin(N,XtN) (1)
av I ändras från en generation till nästa genom att barnen slumpmässigt med återläggning drar sina föräldrar, så att Xt bildar en Markovkedja. Samuel Karlin och Chris Cannings utvecklade sedan mer allmänna modeller, där antalet ”barn” till föräldrarna i generation t också är utbytbara stokastiska variabler, men med större variation än den som följer av (1). Man kan generalisera modellen och låta populationsstorleken variera över tid. Selektion införs i WF-modellen genom att låta genvariant I ha en reproduktiv fördel s > 0 och låta sannolikheten i (1) bli proportionell mot (1+s)XtN+(1-XtN). För att bygga in migration måste man införa geografisk struktur, exempelvis i form av delvis isolerade öar med ett visst genutbyte emellan. Men man kan även införa andra typer av struktur, såsom ålder (genom att definiera livslängdstabeller, på liknande sätt som i livförsäkring), eller kön (genom de mendelska nedärvningslagarna och olika parningsmönster).
Att få in mutationer i modellerna
För modeller med mutationer blir tillståndsrummet mer komplicerat, eftersom nya genvarianter tillkommer. Men delar in de N individerna i ekvivalensklasser beroende på deras genvariant, och låter Xt beskriva tidsdynamiken hos klasstorlekarnas fördelning. Warren Ewens angav i början av 1970-talet en samplingformel, som under vissa antaganden ger jämviktsfördelningen hos selektivt neutrala genvarianter i närvaro av mutationer. Den uppstår som en balans mellan de två mekanismer som strävar efter att minska (genetisk drift) respektive öka (mutationer) den genetiska variationen. Rekombinationer, slutligen, införs när den genetiska variationens tidsutveckling studeras för flera markörer samtidigt, så att Xt blir en vektor där varje element svarar mot en markör.
Hittills har ”tiden” t bara varit en räknare för generation. För stora populationer är det ofta en fördel att införa kontinuerlig tid och approximera Markovkedjan med en stokastisk differentialekvation. Om vi undersöker flera genpositioner samtidigt blir denna SDE vektorvärd, där A) den genetiska driften och rekombinationerna ger elementen i diffusionstermens kovariansmatris, och B) det naturliga urvalet och migrationen orsakar den systematiska driften. Om vi dessutom utökar modellen till att innehålla mutationer blir tillståndsrummet mer komplicerat, som i det tidsdiskreta fallet. Medan Fisher lade grunden för SDE-approximationerna, utvecklade Wright denna teknik vidare, och sedan tog Kimura vid och löste på 1950-talet Kolmogorovs framåt- och bakåtekvationer explicit i flera viktiga fall.
Att vända på tiden
I slutet av 1970-talet skrev Ewens en bok som sammanfattade mycket av den dittills utvecklade matematiska teorin för populationsgenetik. Kort därefter introducerade John Kingman i början av 1980-talet en idé som visade sig vara mycket fruktbar för populationsgenetiken. Hans koalescensteori kan sägas vara en vidareutveckling av att vända på tiden för en Markovkedja. Vi får då en ny Markovkedja. Visserligen hade Charles Cotterman och Gustave Malécot mer än 30 år tidigare infört begreppet identisk härkomst för gener, men Kingman visade hur ett helt genetiskt släktträd är fördelat bakåt i tiden. Detta släktträd är inte en vanlig individbaserad stamtavla, utan ett Markovträd som visar hur olika individers kopior av en gen har ärvts ned längs olika släktlinjer som så småningom sammanstrålar hos en gemensam anfader. Dess utseende beror inte bara på den kromosom vid vilken genen är belägen, utan även (på grund av överkorsningar) på positionen längs denna kromosom. En av de största fördelarna med koalescensteorin är att selektivt neutrala modeller blir mycket enklare att analysera, eftersom endast de mutationer som överlevt till dagens generation tas med, och de kan slumpas ut som en Poissonprocess på släktträdet.
Koalescensteorin har idag utvecklats till en egen disciplin inom sannolikhetsteorin, där Jean Bertoin, Peter Donnelly, Richard Durrett, Simon Tavaré och andra gjort viktiga bidrag, men även flera svenskar, såsom Magnus Nordborg, Peter Jagers, Ingemar Kaj och Serik Sagitov. Den har många tillämpningsområden, och inom populationsgenetiken är den ett fruktbart verktyg för att studera mänsklighetens historia och andra processer bakåt i tiden, där moderna dataset med hundratusentals markörer per individ ger nya möjligheter att jämföra olika modeller. Något mer överraskande är koalescensteorin även mycket användbar för att studera förändringar framåt i tiden, Den kan exempelvis ge framåtrekursioner för den predikterade inavelskoefficienten
ft=P(samma genvariant för två slumpmässigt valda individer, tid t)
och andra av Wright införda storheter. Liksom i filmen Tillbaka till framtiden kan vi med tidsmaskinens hjälp bygga upp (sannolikhetsfördelningen för) ett släktträd bakåt, med start i framtiden.
Risken för inavel
Inom bevarandebiologin studerar man hur den biologiska mångfalden i olika ekosystem kan bevaras. Bara de senaste decennierna har många djurarter antingen dött ut eller blivit starkt hotade, bland annat på grund av ökad inavel som ökar förekomsten av recessiva sjukdomar. För att förhindra detta vill man kunna förutsäga risken för att olika anlagsvarianter går förlorade och hur olika strategier påverkar inavelsförändringen (som djurreservat, fiske, fiskodling, anläggning av dammar, avskjutning av älgar, migration av vargar från Finland och Ryssland). Under det korta tidsperspektiv det här är fråga om är det framför allt genetisk drift, migration och rekombinationer som påverkar. Dessutom verkar de kontinuerliga SDE-approximationerna ofta över för lång tid för att vara användbara. Eftersom risken för ökad inavel är större för små populationer än för stora, används den effektiva populationsstorleken Ne som ett mått på inversen av den takt med vilken inaveln ökar. En vanlig tumregel är Ne≥50 för kortsiktigt bevarande av en population 5-10 generationer framåt i tiden.
Man kan ange Ne på flera olika sätt. En metod är att utgå från hur snabbt sannolikheten ft ökar mot 1. Alternativt kvantifierar man hur snabbt genetisk drift sker. För en genetisk markör med två varianter, blir Ne då inversen av en normaliserad varians
σ2=Var(Xt+1Xt(N-Xt)|Xt)=1Ne,
som kan liknas vid volatiliteten för de processer som studeras i finansiell matematik. En tredje metod utgår från största egenvärdet mindre än 1 hos övergångsmatrisen för Markovkedjan Xt. Det anger hur snabbt ett absorberande tillstånd nås: I ett absorberande tillstånd stannar Markovkedjan där den är och därmed har anlag förlorats. Ett fjärde sätt är att med hjälp av koalescensteorin ange hur snabbt grenarna i trädet går ihop bakåt i tiden. Det visar sig att alla dessa definitioner av Ne överensstämmer med den verkliga populationsstorleken N för WF-modellen. Men oftast är Ne betydligt mindre, speciellt om reproduktiviteten mellan föräldrar varierar mer än vad (1) anger.
Under de senaste åren har jag i min forskning arbetat med att få fram en enhetlig matematisk teori för populationer som av någon orsak är strukturerade. Såväl Markovkedjan Xt som den deterministiska inavelsprocessen ft blir då vektorvärda, och definitionerna av effektiv storlek ger olika värden på Ne. Till exempel visar det sig att alla komponenter hos ft-processen går mot 1 med samma hastighet, och den ges av största egenvärdet hos den matris som ligger till grund för tidsrekursionen från ft till ft+1. Men för kortare tidsperspektiv är det mer intressant att ange hela tidsprofilen för inavelsökningen, och då tar man med matrisens hela spektrum av egenvärden. En del av detta, och annat, beskrivs i den avhandling som Fredrik Olsson försvarade i maj 2015, ett arbete som utförts i samarbete med två populationsgenetiker från Stockholms universitet, Linda Laikre och Nils Ryman.
Ola Hössjer
Stockholms universitet
Skriv ut......



